Introduction to Irrational and Rational Numbers
Numbers play an essential part in mathematics and everyday life, helping us quantify, measure, and solve problems. There are two classifications of numbers within their vast realm – rational and irrational numbers.
Rational numbers can be defined as any ratio between integers; while irrational ones cannot be expressed as fractions and have non-terminating decimal expansions. Rational numbers such as fractions and terminating or repeating decimals provide precise representations and possess distinctive properties such as closure under operations and the existence of inverses.
On the other hand, irrational numbers such as pi or the square root of 2 add depth and richness to our number system. Their decimal representations extend indefinitely without repeating, making them both intriguing and challenging to work with.
Understanding the distinctions between rational and irrational numbers are an integral component of many mathematical applications, from geometry and algebra to mathematical proofs. Understanding their distinctive properties helps us better comprehend their significance when solving problems or exploring numerical reality.
Definition of Numbers
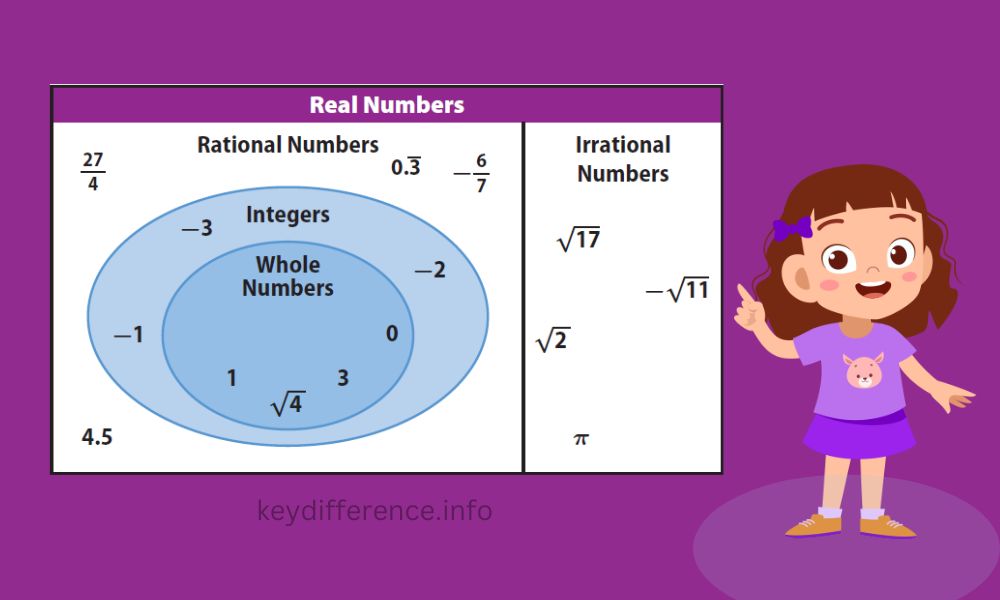
Numbers are mathematical entities used to represent quantities, measurements and relationships mathematically. Numbers allow users to count, measure, compare and perform calculations easily and can be divided into various types based on their properties and characteristics;
such as natural numbers, whole numbers, integers rational numbers irrational and real numbers; with each serving its own purpose with unique properties and operations associated with it – numbers play an essential part in various branches of mathematics science economics and everyday life applications.
Classification of numbers
The properties and characteristics of numbers can be used to classify them into different categories.
There are three main types of number:
- Natural numbers are positive integers that start at 1 and continue indefinitely. They are used to count and order objects.
- Whole numbers include all natural numbers, including zero (zero). Whole numbers do not include decimals or fractions.
- The set of integers includes all whole numbers, their negatives and zero. Positive numbers, negative numbers and zero are included.
- Rational numbers can be expressed by the ratio of two integers, p/q, where q does not equal zero. You can write them as decimals or fractions. Integers and fractions are rational numbers.
- They are not expressed by the ratio between two integers. They are non-repeating, non-terminating decimal numbers. Irrational numbers are the square root of 2, pi (p) and the golden proportion (ph).
- Real numbers are both rational and irrational. They include all points on the number line, such as positive and negative, fractions, decimals and irrational.
- Complex numbers are numbers that can be expressed as a + bi where “a” and b are real numbers and “i” represents the imaginary unit (0-1). Complex numbers are a combination of real and imaginary numbers and they can be used for complex analysis, as well as other mathematical applications.
These classifications help to understand the various types of numbers and their relationship. Each number type has its own properties and operations. It also has different applications in mathematics and other disciplines.
What are Rational Numbers?

Definition and Characteristics
A. Rational numbers can be expressed as fractions with both integer numerators and denominators that do not equal zero as denominators.
B. Rational numbers can also be expressed as terminating decimals (decimals that end) or repeating decimals (decimals that have a repeating pattern).
C. Rational numbers can be positive, negative, or zero.
Examples of Rational Numbers
- Whole numbers: 0, 1, 2, 3, …
- Integers: …, -3, -2, -1, 0, 1, 2, 3, …
- Fractions: 1/2, 3/4, -5/6, 7/3, …
- Terminating decimals: 0.5, 0.75, -1.25, 2.0, …
- Repeating decimals: 0.333…, 0.666…, -0.142857142857…, 1.272727…, …
Properties of Rational Numbers
- Closure under Addition: When you add two rational numbers, the result is always a rational number.
- Closure under Subtraction: When you subtract one rational number from another, the result is always a rational number.
- Closure under Multiplication: When you multiply two rational numbers, the result is always a rational number.
- Closure under Division: When you divide one rational number by another (excluding division by zero), the result is always a rational number.
- Rational numbers can be ordered and compared: You can determine which is greater or lesser by comparing their fractions or decimal representations.
- Rational numbers can be converted: In Different forms, such as converting a fraction to a decimal or a decimal to a fraction.
Applications of Rational Numbers
- Measurements: Rational numbers are used to represent measurements such as lengths, weights, and quantities.
- Financial calculations: Rational numbers are used in calculations involving money, percentages, and interest rates.
- Data analysis: Rational numbers are used to represent and analyze data in statistics and probability.
- Geometry: Rational numbers are used in geometric calculations involving lengths, angles, and coordinates.
- Engineering and construction: Rational numbers are used in engineering and construction to represent measurements and calculations.
Significance of Rational Numbers
- Rational numbers are fundamental to mathematics and provide a foundation for further study of number systems.
- They allow precise representation of quantities and enable accurate calculations in various fields.
- Rational numbers help in understanding and solving real-life problems involving measurements, finance, and data analysis.
- They are essential in fields such as science, engineering, economics, and computer science.
- Rational numbers help develop critical thinking, problem-solving, and mathematical reasoning skills.
What are Irrational Numbers?

Definition and Characteristics
A. Irrational numbers are numbers that cannot be expressed as a fraction. They cannot be written as a ratio of two integers.
B. Irrational numbers have decimal representations that neither terminate nor repeat. They have an infinite number of non-repeating decimal digits.
C. Irrational numbers can be positive or negative.
Examples of Irrational Numbers
- √2 (square root of 2)
- π (pi)
- e (Euler’s number)
- √3 (square root of 3)
- √5 (square root of 5)
- Golden ratio (∅)
Properties of Irrational Numbers
- Irrational numbers are not closed under operations like addition, subtraction, multiplication, and division. The result of these operations can be either rational or irrational.
- Irrational numbers cannot be directly ordered or compared. They do not follow the rules of inequality like rational numbers.
- Irrational numbers can be approximated by rational numbers. By using rational numbers as approximations, we can get closer and closer to the value of an irrational number.
Relationship with Rational Numbers
- Irrational numbers and rational numbers together form a set of real numbers.
- Between any two rational numbers, there is an infinite set of irrational numbers. This shows the density of irrational numbers on the number line.
- Some irrational numbers, such as √2, cannot be expressed as a fraction or a repeating decimal, making them fundamentally different from rational numbers.
Applications of Irrational Numbers
- Geometry: Irrational numbers are used to represent lengths, diagonals, and areas in geometric calculations.
- Trigonometry: Trigonometric functions involve irrational numbers, such as sine, cosine, and tangent.
- Calculus: Irrational numbers are used in calculus to represent limits, derivatives, and integrals.
- Cryptography: Irrational numbers play a role in encryption algorithms used for secure communication.
- Chaos theory: Irrational numbers are involved in chaotic systems and fractals, which have applications in various fields.
Significance of Irrational Numbers
- Irrational numbers expand our understanding of numbers beyond rationality and show the infinite nature of mathematics.
- They are essential in various branches of mathematics and their applications in real-world scenarios.
- Irrational numbers challenge our intuition and provide opportunities for exploration and discovery in mathematics.
- They help us understand the limits of rationality and the rich complexity of the number system.
Differences between Irrational and Rational Numbers
Here are the key differences between irrational and rational numbers:
Representation
- Rational numbers can be expressed as a fraction or a ratio of two integers.
- Irrational numbers cannot be expressed as a fraction or a ratio of two integers.
Decimal Representation
- Rational numbers have decimal representations that are either terminating (end) or repeating (have a recurring pattern).
- Irrational numbers have decimal representations that neither terminate nor repeat. They have an infinite number of non-repeating decimal digits.
Expressibility
- Rational numbers can be precisely expressed using a finite number of digits or as a fraction.
- Irrational numbers cannot be precisely expressed using a finite number of digits or as a fraction.
Closure under Operations
- Rational numbers are closed under addition, subtraction, multiplication, and division. When you perform these operations on rational numbers, the result is always a rational number.
- Irrational numbers are not closed under these operations. Performing addition, subtraction, multiplication, or division with irrational numbers can yield either a rational or an irrational number.
Order and Comparison
- Rational numbers can be ordered and compared directly using inequality symbols (<, >, ≤, ≥).
- Irrational numbers cannot be directly ordered or compared. They do not follow the rules of inequality like rational numbers.
Density
- Rational numbers are dense, meaning between any two rational numbers, there is always another rational number.
- Irrational numbers are also dense, but there are gaps between irrational numbers and rational numbers. Between any two irrational numbers, there are infinitely many rational and irrational numbers.
Example
- Examples of rational numbers include fractions like 1/2, 3/4, and terminating or repeating decimals like 0.75, 0.333…, and whole numbers like 5, -2, etc.
- Examples of irrational numbers include √2 (square root of 2), π (pi), and e (Euler’s number).
Number Line Representation
- Rational numbers can be represented on the number line with evenly spaced points.
- Irrational numbers are represented on the number line as non-repeating, non-terminating points, often requiring approximation.
Understanding these key differences is important for comprehending the unique properties and characteristics of irrational and rational numbers within the broader number system.
Irrational and Rational Numbers: Comparison Chart
Here’s a comparison chart highlighting the main differences between irrational and rational numbers:
| Characteristic | Irrational Numbers | Rational Numbers |
|---|---|---|
| Definition | Real numbers that cannot be expressed as fractions | Real numbers expressed as fractions of integers |
| Examples | π (pi), √2 (square root of 2), e (Euler’s number), √3 | 1/2, -3/4, 0.75 |
| Decimal Representation | Non-terminating, non-repeating decimals | Terminating or repeating decimals |
| Arithmetic Operations | Can be involved in operations with rational numbers | Can be operated on using standard arithmetic operations |
| Closure Property | Not closed under addition, subtraction, multiplication | Closed under addition, subtraction, multiplication |
| Order and Comparison | Can be compared using inequality symbols | Can be compared using inequality symbols |
| Number Line Placement | Can be located between rational numbers on the number line | Can be located between irrational numbers on the number line |
| Density | Form a dense set on the number line | Form a dense set on the number line |
| Algebraic Properties | Cannot be expressed as an exact solution to polynomial equations | Can be expressed as an exact solution to polynomial equations |
| Square Roots | Square roots of non-perfect squares are irrational | Square roots of perfect squares are rational (e.g., √4 = 2) |
| Practical Applications | Geometry, trigonometry, chaos theory, quantum mechanics, irrational calculus | Arithmetic calculations, measurements, finance, data analysis, statistical calculations, etc. |
Similarities between rational and irrational numbers
While rational and irrational numbers are distinct in their properties, there are a few Similarities between them:
- Both are Real Numbers: Rational and irrational numbers are both subsets of the real number system. They are used to represent quantities and measurements in the physical world.
- Infinite Decimal Representations: Both rational and irrational numbers can have infinite decimal representations. Rational numbers can have repeating or terminating decimals, while irrational numbers have non-repeating, non-terminating decimals.
- Existence Between Two Rational Numbers: Between any two rational numbers, there exists an infinite set of both rational and irrational numbers. This property, known as density, is shared by both types of numbers.
- Existence of Irrational Components in Some Rational Numbers: Certain rational numbers can have irrational components. For example, √2 can be part of a rational number when it is expressed in simplest radical form.
- Mathematical Operations: Rational and irrational numbers can be involved in mathematical operations together. For example, adding a rational number to an irrational number can result in an irrational number.
- Coexistence on the Number Line: Rational and irrational numbers coexist on the number line. They are interspersed and can be visualized as points on the same continuum, even though their distribution may differ.
It is important to note that while rational and irrational numbers share these similarities, their distinct properties set them apart and give rise to unique characteristics and behaviors in mathematical contexts.
Irrational and Rational Numbers: Applications in Mathematics
Irrational and rational numbers have significant applications in various branches of mathematics.
Here are some specific applications:
Irrational Numbers
- Geometry and Trigonometry: Irrational numbers, such as √2 and π, appear in geometric calculations and trigonometric functions. For example, the diagonal of a square with sides of length 1 has a length of √2, and the circumference of a circle with a radius of 1 is given by 2π.
- Number Theory: Irrational numbers are often studied in number theory, which explores the properties and relationships of numbers. They provide examples of numbers that cannot be expressed as fractions or ratios.
- Mathematical Analysis: Irrational numbers are central to mathematical analysis, including calculus and real analysis. They are used to define limits, continuity, and differentiation. For example, the concept of limits involves approaching an irrational number without ever reaching it.
- Chaos Theory and Fractals: Irrational numbers play a role in chaos theory and the study of fractals, which deal with complex and unpredictable patterns. The Mandelbrot Set, a famous fractal, involves the iteration of complex numbers, including irrational ones.
Rational Numbers
- Arithmetic and Algebra: Rational numbers are extensively used in arithmetic operations and algebraic manipulations. They are used to solve equations, simplify expressions, and perform calculations involving fractions.
- Proportions and Ratios: Rational numbers are crucial in representing and comparing proportions and ratios. They are employed in various real-world scenarios, such as scaling, proportions in recipes, and financial ratios.
- Data Analysis and Statistics: Rational numbers are utilized in statistical analysis to represent discrete quantities and measurements. They are used to calculate means, medians, and proportions, as well as to construct and interpret graphs and charts.
- Probability Theory: Rational numbers are utilized in probability theory to represent probabilities and probabilities of events. They play a role in determining the likelihood of outcomes in various random experiments.
Both irrational and rational numbers are indispensable in mathematics, providing the foundation for different areas of study and enabling precise calculations, modeling, and analysis. Understanding their properties and applications is essential for advancing mathematical knowledge and its practical implementation.
Irrational and Rational Numbers: Applications in Science and physics
Irrational and rational numbers have applications in various scientific disciplines, including physics.
Here are some specific applications:
Irrational Numbers
- Measurement and Uncertainty: Irrational numbers, such as √2 and π, are used in measurements and calculations involving uncertainty. They allow for more precise representations of physical quantities and help account for the inherent uncertainty in measurements.
- Wave Phenomena: Irrational numbers, particularly π, are involved in wave phenomena and oscillations. They appear in the equations describing waveforms, wave propagation, and interference patterns, such as in the equations for the motion of a pendulum or the wave equation itself.
- Quantum Mechanics: Irrational numbers are intrinsic to the mathematical framework of quantum mechanics. They appear in the solutions to Schrödinger’s equation, which describes the behavior of quantum systems, including atomic and subatomic particles.
Rational Numbers
- Kinematics and Dynamics: Rational numbers are used in classical mechanics to describe the motion and forces acting on objects. Quantities such as velocities, accelerations, and forces are often represented by rational numbers.
- Thermodynamics: Rational numbers are used in thermodynamics to represent temperatures, pressures, and other thermodynamic properties. They are involved in calculations related to energy transfer, heat flow, and the behavior of gases and fluids.
- Electrical Circuits: Rational numbers are applied in electrical circuits to represent voltage, current, resistance, and other electrical quantities. Rational numbers are used in calculations involving Ohm’s law, Kirchhoff’s laws, and circuit analysis.
- Data Analysis and Statistics: Rational numbers are employed in scientific data analysis and statistics. Rational numbers are used to represent discrete measurements, experimental results, and statistical values such as means, standard deviations, and probabilities.
By utilizing both irrational and rational numbers, scientists and physicists can accurately describe physical phenomena, make precise calculations, and develop mathematical models to explain the natural world. These numbers provide the necessary mathematical foundation to understand and analyze various scientific principles and theories.
Importance in practical situations and everyday life

Irrational and rational numbers play important roles in practical situations and everyday life.
Here are some examples of their significance:
Irrational Numbers
- Measurements: Irrational numbers, such as √2 and π, are used in precise measurements. They allow for accurate representations of lengths, areas, volumes, and other physical quantities. For instance, when constructing buildings or designing objects, precise measurements involving irrational numbers are essential to ensure proper dimensions.
- Finance and Economics: Irrational numbers are relevant in financial and economic calculations. They are used in interest rate calculations, investment evaluations, and risk assessments. For example, compound interest calculations involving irrational numbers are essential in determining long-term savings and investment growth.
- Design and Aesthetics: Irrational numbers are employed in design and aesthetics to achieve aesthetically pleasing proportions and ratios. Concepts such as the golden ratio (∅) and the Fibonacci sequence, which involve irrational numbers, are utilized in art, architecture, and graphic design to create visually appealing compositions.
Rational Numbers:
- Fractional Measurements: Rational numbers, expressed as fractions, are used to represent fractional measurements in various contexts. Cooking recipes, construction plans, and DIY projects often rely on rational numbers to determine precise quantities and proportions.
- Budgeting and Personal Finance: Rational numbers are practical in everyday financial situations. They are used in budgeting, expense tracking, and calculating percentages. Rational numbers allow for precise calculations when dealing with income, expenses, savings, and debt management.
- Unit Conversions: Rational numbers facilitate unit conversions in everyday life. Whether converting units of length, weight, time, or other measurements, rational numbers enable accurate and consistent conversions between different systems of measurement.
- Probability and Statistics: Rational numbers are employed in probability and statistics for practical applications. They are used to represent probabilities, odds, and statistical data in fields such as risk analysis, market research, and sports analytics.
Understanding and utilizing both irrational and rational numbers is crucial for making accurate measurements, performing calculations, making informed decisions, and solving everyday problems. These numbers are embedded in various aspects of our lives, from financial planning to cooking, construction, and aesthetic design.
Recap of the Irrational and Rational Numbers
Rational numbers are a subset of real numbers that can be expressed as fractions, while irrational numbers are real numbers that cannot be expressed as fractions. Rational numbers can have decimal representations that either terminate or repeat, while irrational numbers have decimal representations that neither terminate nor repeat.
Rational numbers can be operated on using standard arithmetic operations and are closed under these operations, resulting in another rational number. Irrational numbers can be involved in mathematical operations with rational numbers, yielding an irrational number.
Both types of numbers coexist on the number line and have practical applications in various mathematical fields and real-world scenarios. Understanding irrational and rational numbers is essential for accurate mathematical representations and calculations.

